Benign Overfitting beyond Prediction

Letian Yang, Dennis Shen

Motivation

Modern machine learning has challenged classical statistical intuition: deep models with far more parameters than data can generalize well despite overfitting — a phenomenon known as benign overfitting (Zhang et al., 2017; Belkin, 2021). High-dimensional linear regression plays a key role in understanding this behavior (Bartlett et al., 2020a; Hastie et al., 2022).

Double Descent Curve

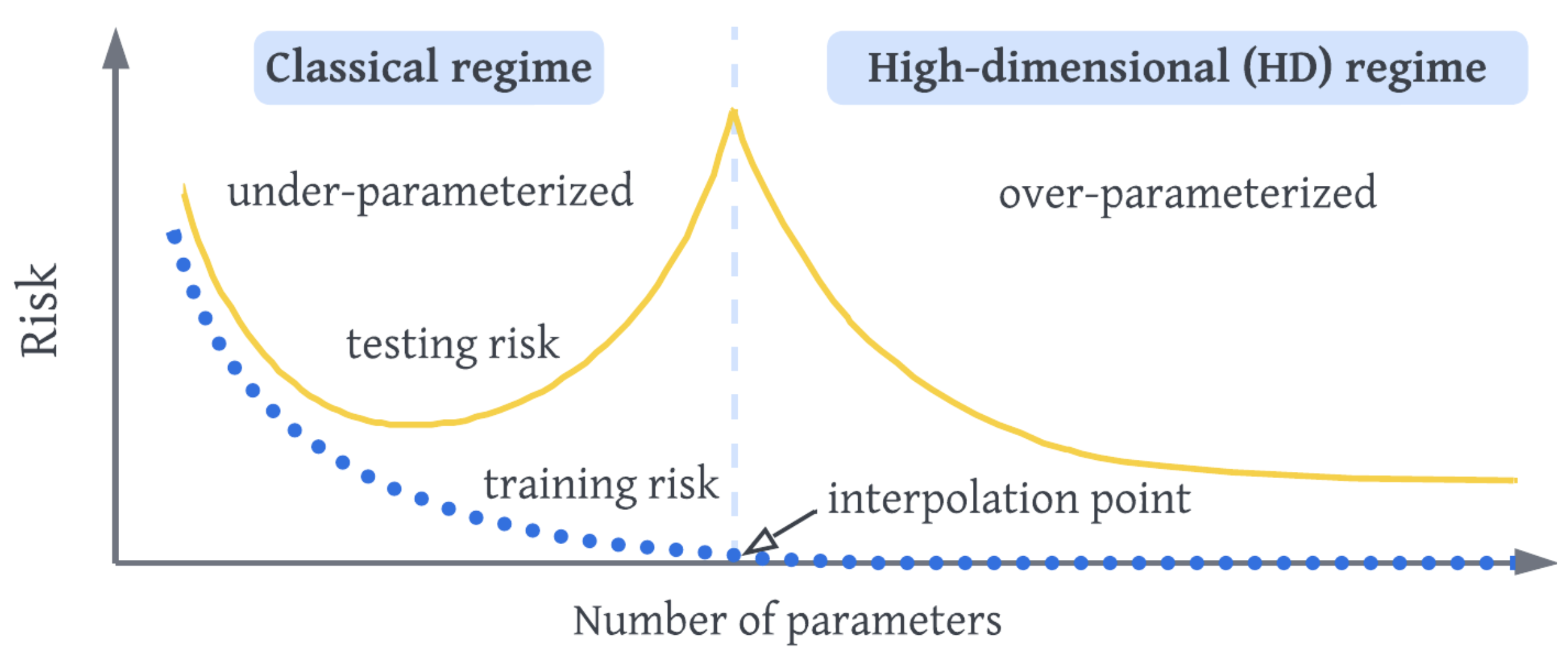
While much of the existing theory focuses on prediction, many scientific fields — especially causal inference, econometrics, and the social sciences — rely not only on predicting outcomes but also on estimating interpretable parameters such as treatment effects. This raises a natural and largely unresolved question:

Can we still trust overparameterized least squares for parameter estimation and inference?


To investigate this, we study a variant of the ordinary least squares (OLS) interpolator in which only a subset of coefficients is implicitly regularized, a setting we refer to as partial regularization. This framework mirrors modern causal workflows where a treatment coefficient must remain unregularized for interpretability, while high-dimensional nuisance covariates may be effectively penalized.

We leave θ* and β₀* un-regularized.

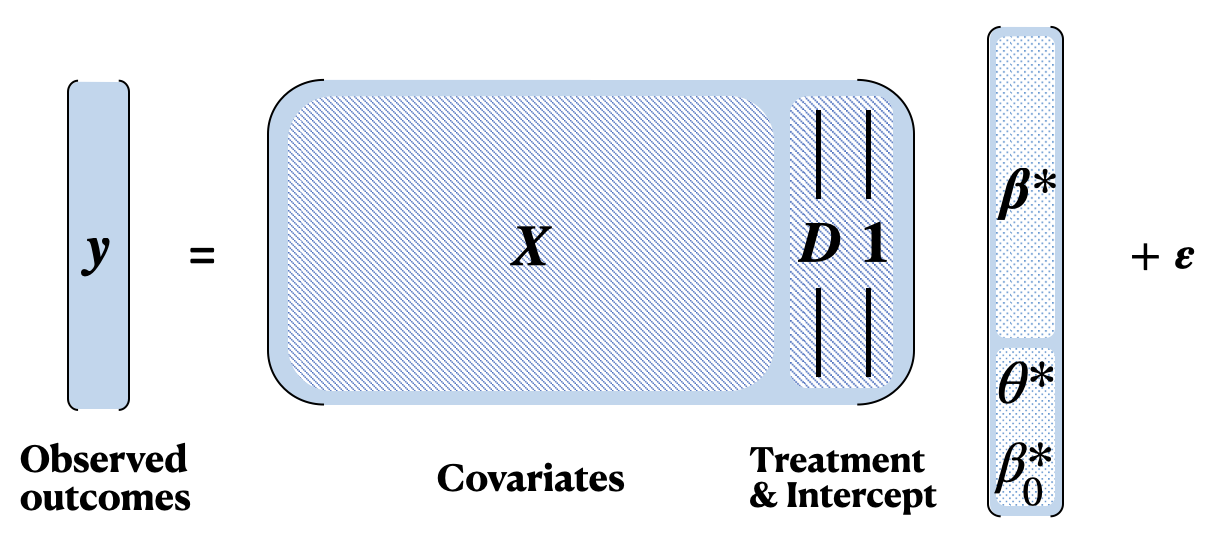
What We Achieve

This project extends the study of benign overfitting beyond prediction, offering:

  • New algebraic identities that clarify how partial regularization reshapes OLS
  • Variance estimation tools for inference in high-dimensional regression
  • Conceptual bridges between benign overfitting and modern causal estimation
  • Empirical evidence that interpolating estimators can remain useful for parameter estimation

Together, these results suggest that overparameterization does not inherently preclude valid inference, provided appropriate structure and regularization are present.

Publication Status

A manuscript based on this work is currently under submission to AISTATS 2026, and another is available on arXiv.

Future Directions

This project contributes to a broader effort to understand:

  • High-dimensional linear models
  • Overparameterization and interpolation
  • Causal inference in modern regimes

If you are interested in collaborating or discussing related topics, feel free to reach out!